Time mixed with the power of compounding is the most potent combination for wealth creation.
Compound interest allows you to grow wealth faster by earning a return on your past returns. This isn’t a linear relationship – it’s exponential. The human brain isn’t good at visualizing exponential things, which may explain why it’s so difficult to fully appreciate a plan that fully leverages the power of compounding.
Let’s try to fix that.
Imagine you take a sheet of standard printer paper with a thickness of 0.1 mm.
Fold it over once and it gets twice as thick. Fold it again and you’ve doubled the thickness of the paper again; two folds make the paper four times as thick. Fold it a third time and now the paper is eight times as thick.
If you could fold that piece of paper 50 times, the paper would stretch 95 million miles or approximately the distance from Earth to the sun.
At 100 folds, it matches the radius of the universe.
Unfortunately, it isn’t possible to fold a piece of paper more than eight times (try, I dare you). But the underlying math of repeatedly doubling the thickness of paper is exciting when we apply the same exponential growth to your savings.
The Rule of 72
How many times can you double your money during your lifetime?
That depends on your age and rate of return. With these inputs, we can use a rule of thumb known as The Rule of 72.
Simply assume a reasonable rate of return for planning purposes (between 7 percent and 9 percent over a multi-decade time period) and divide 72 by that rate. This calculates the time it would take for your money to double.
(The Rule of 72 is an approximation. The equation is 2 = 1 x (1 + Rate of Return)Y, where Y is the time to double.)
To make the math nice and even, let’s say we earn an 8 percent return on your money. According to the Rule of 72, it takes nine years to double your money (72 ÷ 8 = 9).
Ready for the compounding part?
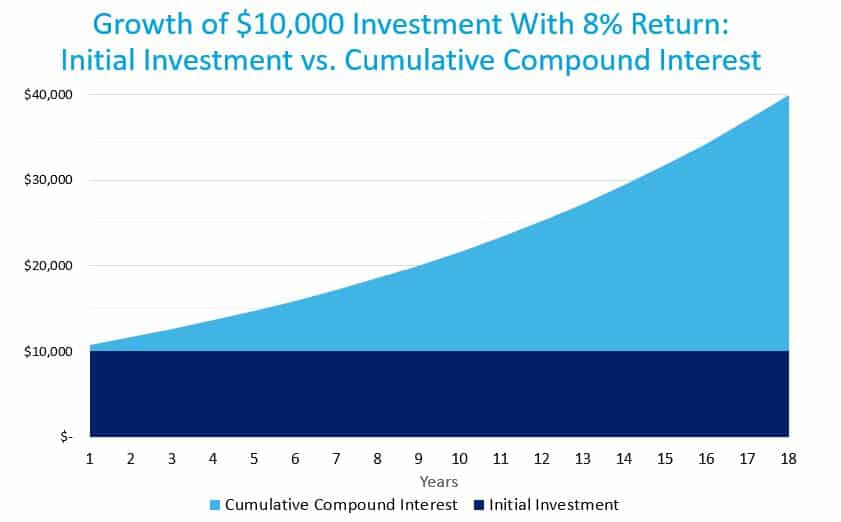
Let’s start with $10,000 and continue to assume we earn a return of 8 percent.
After nine years, the Rule of 72 tells us we will have $20,000. It should seem obvious that the $20,000 then takes another nine years to double, so we will have $40,000 after 18 years. Over time, the earnings on interest becomes disproportionately larger than the earnings on the initial investment.
To see how good planning can maximize the benefit of compound interest, we can draw from Benjamin Franklin’s financial plan.
How Benjamin Franklin Leveraged the Power of Compounding in His Financial Plan
At his death, Franklin’s will left 1,000 pounds sterling (then worth about $9,000) to his adopted home of Philadelphia and his native city, Boston.
Franklin wanted trustees to loan the money to apprentices, much in the same way he received assistance early in his career. His will also stipulated that the interest collected from the loans should stay invested so it could compound over time.
After 100 years, both cities could withdraw 75 percent of the funds to use for infrastructure projects that would improve the quality of life for those living in these cities like bridges, roads, water systems, and public buildings.
Then in another 100 years, the cities could withdraw the remaining balance for additional infrastructure and city betterment projects.
Franklin estimated a 5 percent annual rate of returns from the loans. It turned out to be 4 percent. He was off by one percentage point, but remember that financial success depends less on marginally higher returns than it does on saving and time. This case serves as a perfect example of this phenomenon.
The cities made their first withdrawals in 1890. The fund grew from Franklin’s initial contribution of $9,000 to $500,000 over a period of 100 years (that’s about $13 million in today’s dollars).
When the cities could make their second withdrawal in 1990, they gained access to another $6.5 million (or $12 million in today’s dollars).
Franklin understood the power of compounding and knew that good planning and time were the essential ingredients to having it work in your favor.
You probably won’t get to work with a 100-year time horizon, but you will get several decades to allow your investments to earn compound returns if you start saving now.
The way Franklin structured his will provides a great illustration of how thoughtful planning and time can best capture the power of compounding. The more time you have, the more your wealth benefits from this compounding effect.
Once you create a well-thought-out financial plan that focuses on maximizing your wealth as a means to meet your goals, you can sit back and let time do its thing.
Resource: Need help putting together a well-thought-out financial plan? Let’s talk.
Small Decisions and Good Habits Lead to Big Results
It’s simple to achieve financial success if you can make decisions that take advantage of the power of compounding over time.
Whether you’re saving early and often, systematically adding to your investment portfolio, or staying the course in times of uncertainty, time has the power to turn small habits into incredible results.
The problem is there are lots of decisions to make…
- Should you invest or pay down debt?
- Where should you keep cash savings?
- What types of investment accounts should you use first?
- Should you rent or buy a home?
The decisions you make today will have compounded effects decades later. But before you can start making good choices, you first must take time to figure out what you’re trying to get out of life.
This material has been prepared for informational purposes only and should not be used as investment, tax, legal or accounting advice. All investing involves risk. Past performance is no guarantee of future results. Diversification does not ensure a profit or guarantee against a loss. You should consult your own tax, legal and accounting advisors.
